Definição de Função

Sejam \( A \) e \( B \) dois conjuntos não vazios. Uma função \( f \) de \( A \) para \( B \), representada como \( f:A \to B \), é uma regra que liga cada elemento de \( A \) a exatamente um elemento de \(B\).

Domínio, Contradomínio e Imagem

Exemplo:

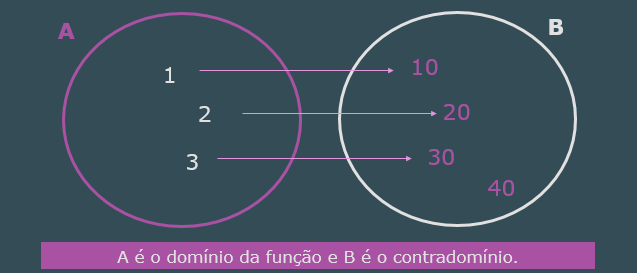
• Domínio: \( A = \{1, 2, 3\} \)
• Contradomínio: \( B = \{10, 20, 30, 40\} \)
• Imagem: \( \text{Im}(f) = \{10, 20, 30\} \)
• X ∈ A e Y ∈ B

A função pode ser definida por:

$$ f(x) = 10x $$

Análise Gráfica

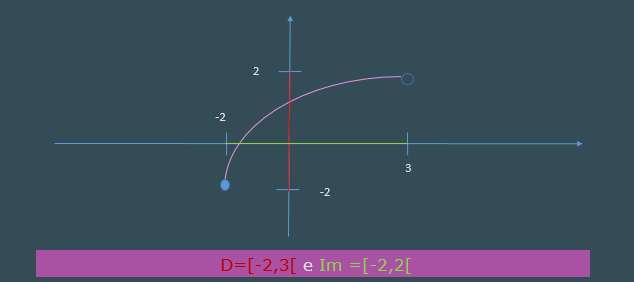
Ao analisar um gráfico, podemos encontrar o domínio e a imagem observando os valores de \(x\) e \(y\), que a função atinge. Os pontos com círculo cheio estão incluídos no domínio/imagem, enquanto os pontos com círculo vazio não estão.

Função Constante

A fórmula geral da função constante é \(f(x)=c\), que significa que para cada valor do Domínio o valor da Imagem se manterá o mesmo, ou seja, para cada valor de \(x\) o \(y\) será o mesmo.

Exemplo:

Função Linear

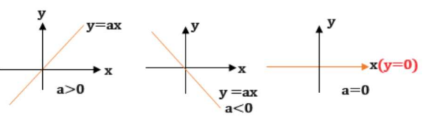
Uma função linear \(f(x)=ax\) tem gráfico em forma de reta que passa por \((0,0)\) e \((1,a)\). Seu comportamento depende de \(a\).

Função Afim

A função afim é representada pela seguinte função: \(f(x)= ax+b\). Assim como a função linear seu comportamento gráfico também depende de \(a\), o qual deve ser diferente de 0. Sendo \(a\) chamado de coeficiente angular e \(b\) de coeficiente linear.

O gráfico a seguir representa a função:

$$ f(x)= 2x + 1 $$

Como montar o gráfico da função afim:

• Identifique os elementos da função:

2 é o coeficiente angular (inclinação da reta).

1 é o coeficiente linear (interseção com o eixo y).

• Encontre o ponto de interseção com o eixo y:

Substitua x = 0 na função: \(f(0)=2(0)+1=1\)

O ponto é \((0,1)\)

• Escolha outro valor de x para encontrar um segundo ponto:

Exemplo: Para x=1, \(f(1)=2(1)+1=3\)

O ponto é \((1,3)\).

Encontrar a função a partir do gráfico

• Identifique a interseção com o eixo y (coeficiente linear):

No gráfico, observe onde a reta cruza o eixo y. O valor de y nesse ponto é o valor do coeficiente linear (\(b\)).

No caso de \(f(x)=2x+1\), a reta cruza o eixo y no ponto \((0,1)\), logo \(b=1\).

• Identifique a inclinação da reta (coeficiente angular):

A fórmula do coeficiente angular é: \[ a = \frac{y - y_{0}}{x - x_{0}} \]

• ​​No gráfico, observe dois pontos quaisquer na reta, como \((0,1)\)e \((1,3)\).

Substituindo os valores na fórmula: \[ a=\frac{3-1}{1-0} \] \[ a=2. \]

Logo, \(a=2\) e \(b=1\), sendo assim, a função que o gráfico representa é: \(f(x)= 2x+1\)

Raíz da Função

É o valor que torna a função zero.

Exemplo: \[ f(x) =\ 2x\ +\ 1 \] \[ 0 =\ 2x\ +\ 1 \] \[ x=-\frac{1}{2} \]

Função Quadrática

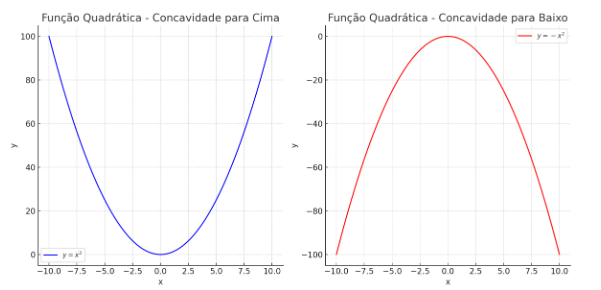
Uma função quadrática \(f:R\rightarrow R\) é uma função da forma \(f(x)=ax^2+bx+c\) onde a, b e c são números reais e \(a≠0\). Seu gráfico é representado por uma parábola, se o \(a\) (coeficiente angular) for positivo a concavidade será para cima, caso seja negativo a concavidade será para baixo.

Como montar o gráfico da função quadrática:

• Achar as raízes:

Igualar a função a zero e resolver a equação de segundo grau. Essas raízes serão a intersecção do gráfico com o eixo X.

• Achar o vértice:

\[ x_{v}=\frac{-b}{2a} \] \[ y_{v} =\frac{-\Delta }{4a} \]

• Determinar o ponto onde a parábola cruza o eixo y

Para encontrar o ponto de interseção com o eixo y, basta substituir x=0 na equação.

Exemplo: \( y=x^{2} -4x+3\)

• 1° Encontrar as raízes:

\begin{array}{l} \Delta =b^{2} -4ac\\ \Delta =( -4)^{2} -4.( 1) .( 3)\\ \Delta =16-12\\ \Delta =4 \end{array}




\begin{array}{l} x=\frac{-b\pm \sqrt{\delta }}{2a}\\ \\ x_{1} =\frac{-( -4) +\sqrt{4}}{2.( 1)} =\frac{4+2}{2} =\frac{6}{2} =3\\ \\ x_{2} =\frac{-( -4) -\sqrt{4}}{2.( 1)} =\frac{4-2}{2} =\frac{2}{2} =1 \end{array}

• 2° Encontrar os vértices:

\begin{array}{l} x_{v} =\frac{-b}{2a}\\ \\ x_{v} =\frac{-( -4)}{2.( 1)} =\ \frac{4}{2} =\ 2\\ \\ y_{v} =\frac{-\delta }{4a}\\ \\ y_{v} =\frac{-4}{4.( 1)} =\frac{-4}{4} =-1 \end{array}

Função Exponencial

A função exponencial de base a é uma função que pega um número real x e calcula \(f(x)=a^x\), onde a é um número positivo diferente de 1 (ou seja, \(a>0\) e \(a≠1\)), e x pode ser qualquer número real. A base a é o número que é elevado à potência x.

Como montar o gráfico da função exponencial:

Exemplo: \[ f(x)=2⋅2^x \]

• Identifique os Parâmetros:

  \(a=2\) (coeficiente).

  \(b=2\) (base da exponencial, como \(b>1\), a função é crescente).

• Calcule Pontos Chave:

  Escolha valores para x (por exemplo, -2, -1, 0, 1, 2).

  Calcule \(f(x)\) para cada x.

• x = -2

\[f( -2) =\ 2.2^{-2} =2.\left(\frac{1}{4}\right) =0,5\]

• x = -1

\[f( -1) =2.2^{-1} =2.\left(\frac{1}{2}\right) =1\]

• x = 0

\[ f( 0) =2.2^{0} =2.1=2 \]

• x = 1

\[ f( 1) =2.2^{1} =2.2=4 \]

• x = 2

\[ f( 2) =2.2^{2} =2.4=8 \]

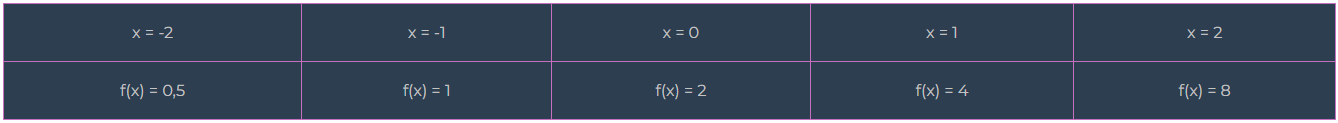
Logarítmo de Número Real

Dados dois números reais \(a > 0\), \(a ≠ 1 \) e \(β > 0\), existe um único número \(y\) tal que \(a^y = β\). Esse número \(y\) é chamado de logaritmo de β na base \(a\) e é representado por: \(y = \log_a \beta\) significa que \(a^y=\beta\)

Exemplos:

• \(\log_{a} 1=0\), pois \(a^{0}=1\)
• \(\log_{a} a=1\), pois \(a^{1}=a\)
• \(\log_{\frac{1}{a}} a=-1\), pois \( (a^{-1})^y = a, a^{-y} = a, -y = 1, y = -1\)
• \(\log_{100} 0,1=-\frac{1}{2}\), pois \( (10^{2})^{y} =10^{-1}, y=-\frac{1}{2}\)
• \(\log 100=2\), pois \( (10)^{y} = (10^{2}), y=2\)
• \(\ln =1\), logaritmo natural, pois \(e^1=e\)

Função Logarítmica

A função logarítmica é representada da seguinte forma : \(f(x)= logₐ⁡β\), sendo que base b deve ser positiva e diferente de 1. O Domínio da função logaritmica compreende somente os reais positivos (sem incluir o zero), já sua Imagem abrange todos os reais

\(b>1\), função é crescente

\( 0 < b < 1 \), função é decrescente