Continuidade e Limite
Conceito intuitivo de Continuidade
Uma função é contínua em um ponto \(x = p\) se seu gráfico não apresenta "saltos" nesse ponto(significa que seu gráfico pode ser desenhado sem tirar o lápis do papel). Isso significa que, ao nos aproximarmos de \(p\), os valores da função também se aproximam de \(f(p)\). Simbolicamente, isso é escrito como: \[ \lim_{x \rightarrow p} f(x) = f(p) \]
Se houver um salto no gráfico em \(x=p\) , a função será descontínua nesse ponto.
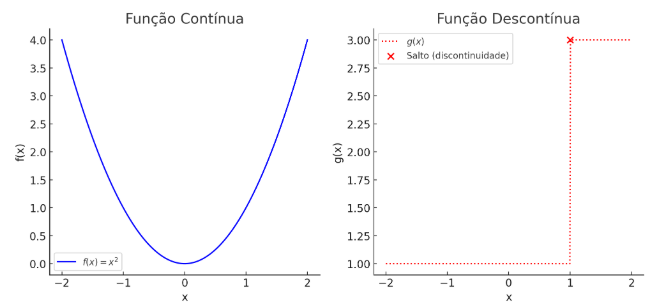
No primeiro gráfico, vemos a função \(f(x) = x^2\), que é contínua porque seu gráfico não apresenta saltos. Conforme x se aproxima de qualquer ponto p, os valores de \(f(x)\) também se aproximam de \(f(p)\).
No segundo gráfico, temos uma função com um salto em \(x = 1\). Para valores menores que 1, \(g(x) = 1\), e para valores maiores ou iguais a 1, \(g(x) = 3\). Isso cria uma descontinuidade porque, ao nos aproximarmos de \(x = 1\) pela esquerda \(x\rightarrow 1^{-}\), \(g(x)\) vale 1, mas pela direita \(x\rightarrow 1^{+}\), \(g(x)\) vale 3. Como os limites não coincidem, a função é descontínua nesse ponto.
Reconhecimento de uma função contínua sem o auxílio do gráfico
Tabela de funções contínuas básicas

Propriedades operatórias com funções contínuas:
- A soma de duas funções contínuas também é contínua
- Multiplicar uma função continua por um número mantém a continuidade.
- O produto de duas funções contínuas continua sendo uma função continua
- O quociente (divisão) de duas funções contínuas também é contínuo, desde que o denominador não seja zero.
- Se \(y=f(u)\) e \(u=g(x)\) forem continuas, então a função composta \(h(x)=f(g(x))\) também será continua.
Importante:
- Só podemos analisar continuidade em pontos que pertencem ao domínio da função.
- Quando dizemos que uma função é contínua, significa que ela não tem "saltos" em nenhum ponto do seu dominio.
Exemplos:

\[ \lim _{x\rightarrow 0}\left( 3-7x+5x^{2}\right) \]
Substituindo \( x = 0 \):
\[ 3 - 7(0) + 5(0)^2 = 3 \]
\[ \lim _{x\rightarrow -1}\left[( x+4)^{3} \cdot ( x+2)^{-1}\right] \]
Substituindo \( x = -1 \):
\[ (-1 + 4)^3 \cdot (-1 + 2)^{-1} \]
\[ (3)^3 \cdot (1)^{-1} \]
\[ 27 \cdot \frac{1}{1} = 27 \cdot 1 = 27 \]
\[ \lim _{t\rightarrow 2}\frac{t^{2} -5t+6}{t-2} \]
Substituindo \( t = 2 \):
\[ \frac{(2)^2 - 5(2) + 6}{2 - 2} \]
\[ \frac{4 - 10 + 6}{2 - 2} \]
\[ \frac{0}{0} \]
Isso está correto?
Não! \(\frac{0}{0}\) é uma indeterminação e não um valor definido.
É necessário fazer uma fatoração, neste caso vamos utilizar soma e produto:
\[ {t^{2} -5t+6} \]
\[ \begin{array}{l} x_{1} +x_{2} =\frac{-b}{a} =\frac{-( -5)}{1} =5\\ \\ x_{1} .x_{2} =\frac{c}{a} =\frac{6}{1} =6\\ \\ 2+3=5\\ \\ 2.3=6 \end{array} \]
Depois pega o sinal de meio, ficando \((t-2).(t-3)\)
\[ \lim _{t\rightarrow 2}\frac{t^{2} -5t+6}{t-2} \]
Fatorando o numerador:
\[ \lim _{t\rightarrow 2}\frac{( t-2) \cdot ( t-3)}{t-2} \]
Cancelando o termo \( t-2 \):
\[ \lim _{t\rightarrow 2} ( t - 3 ) \]
Substituindo \( t = 2 \):
\[ 2 - 3 = -1 \]
\[ \lim _{t\rightarrow 2}\frac{t^{2} -5t+6}{t-2} =\lim _{t\rightarrow 2}\frac{( t-2) .( t-3)}{t-2} =\frac{( 2-2) .( 2-3)}{2-2} =-1 \]
Limite com indeterminação
O limite de uma função f(x) quando x tende a p representa o valor que f(x) se aproxima conforme x se aproxima de p. Se a função for contínua em p, então o limite é simplesmente f(p). No entanto, em alguns casos, ao tentar calcular diretamente, encontramos indeterminações, como \(\frac{0}{0}\). Para resolver isso, utilizamos técnicas algébricas, como a fatoração, para simplificar a expressão antes de substituir o valor de x. Os produtos notáveis são expressões algébricas padronizadas, como quadrados e diferenças de termos, que facilitam a fatoração e ajudam a eliminar termos indeterminados, permitindo o correto cálculo do limite.

Propriedades operatórias dos limites
Seja uma constante e sejam f(x) e g(x) funções tais que: \(\lim _{x\rightarrow p} f( x) =L_{1}\) e \(\displaystyle \lim _{x\rightarrow p} g( x) =L_{2}\). Nessas condições tem-se que:

Exemplos:
Suponha que: \(\displaystyle \lim _{x\rightarrow 2} \ f( x) =\ 4\) e \( \lim_{x\rightarrow{}2} g(x)= -3\)
a) \(\displaystyle \lim _{x\rightarrow 2} \ 7f( x) =\ 7.4=28\)
b) \(\displaystyle \lim _{x\rightarrow 2} \ -2g( x) =-2( -3) =6\)
c) \(\lim _{x\rightarrow 2} \ 5f( x) +\ 4g( x) \)
Substituindo os valores de \( f(2) = 4 \) e \( g(2) = -3 \):
\[ 5 \cdot 4 + 4 \cdot (-3) \]
\[ 20 - 12 = 8 \]
\(\displaystyle \lim _{x\rightarrow 2} \ 5f( x) +\ 4g( x) =\ 5.( 4) \ +\ 4.( -3) =20-12=8\)
Limites Laterais
Definição
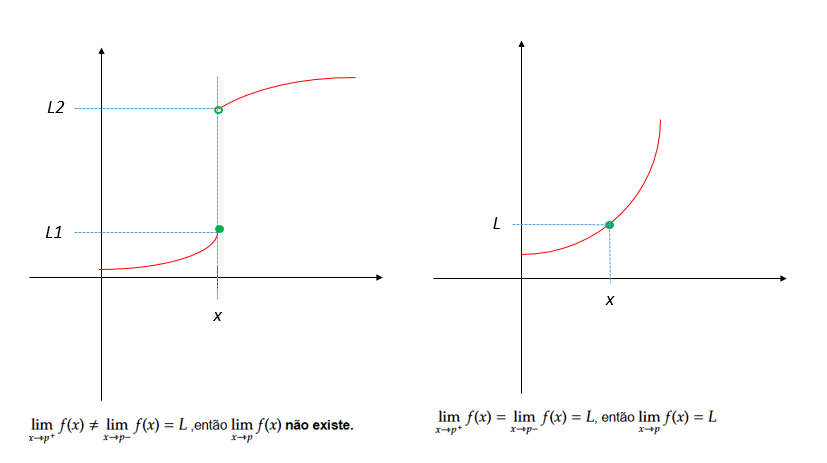
Quando x se aproxima de p por valores maiores que p, o limite de f(x) é \(L_{1}\)
Quando x se aproxima de p por valores menores que p, o limite de f(x) é \(L_{2}\)
Condições para Existência do Limite
Observação:
Se f(x) não estiver definida em um dos lados de p, o limite de f(x) nesse ponto será igual ao limite existente.
Exemplos:
\(\displaystyle f( x) \ =\ \begin{Bmatrix} x\ se\ x\geq 1 & \\ -x\ se\ x< \ 1 & \end{Bmatrix}\), determine os limites \(\displaystyle \lim _{x\rightarrow 1^{+}} f( x)\) e \(\displaystyle \lim _{x\rightarrow 1^{-}} f( x)\)
Precisamos determinar os limites laterais e o limite geral em x=1
1. Cálculo dos limites laterais
Quando x tende a 1 pela direita (x > 1), a função segue a regra f(x) = x. Portanto:
\[ \displaystyle \lim _{x\rightarrow 1^{+}} f( x) =\ \lim _{x\rightarrow 1^{+}} x=1 \]
Quando x tende a 1 pela direita (x < 1), a função segue a regra f(x)=-x
\[ \displaystyle \lim _{x\rightarrow 1^{-}} f( x) =\ \lim _{x\rightarrow 1^{-}} -(x)=-1 \]
2. Verificação do limite geral \(\displaystyle \lim _{x\rightarrow 1} f( x)\)
Para que o limite de f(x) em x = 1 exista, os limites laterais devem ser iguais.
Como \(\displaystyle \lim _{x\rightarrow 1^{+}} f( x) =\ 1\) e \(\displaystyle \lim _{x\rightarrow 1^{-}} f( x) =\ -1\), temos que:
\[ \lim _{x\rightarrow 1^{+}} f( x) \neq \ \lim _{x\rightarrow 1^{-}} f( x) \]
Portanto, o limite \(\displaystyle \lim _{x\rightarrow 1} f( x)\) não existe.
Limites Infinitos
Limites infinitos ocorrem quando, ao nos aproximarmos de um certo valor de \( x \), a função cresce ou decresce sem limite, ou seja, tende ao infinito (\( +\infty \)) ou ao menos infinito (\( -\infty \)).
Isso normalmente acontece em funções racionais (frações) onde o denominador tende a zero, e o numerador permanece diferente de zero ou tende a algum valor fixo.
Exemplo 1:
\[ \lim_{x \to 1} \frac{1}{x-1} \]
Quando \( x \) se aproxima de 1 pela direita:
Valores como 1.1, 1.01, 1.001...
O denominador \( x-1 \) é positivo e muito pequeno.
Isso faz com que \( \frac{1}{x-1} \) fique muito grande positivamente.
\[ \lim_{x \to 1^+} \frac{1}{x-1} = +\infty \]
Quando \( x \) se aproxima de 1 pela esquerda:
Valores como 0.9, 0.99, 0.999...
O denominador \( x-1 \) fica negativo e pequeno.
A fração diminui sem limite.
\[ \lim_{x \to 1^-} \frac{1}{x-1} = -\infty \]
Exemplo 2:
\[ \lim_{x \to 2} \frac{1}{(x-2)^2} \]
Tanto pela esquerda quanto pela direita, o denominador tende a zero positivo (porque está elevado ao quadrado).
A fração cresce sem limite:
\[ \lim_{x \to 2} \frac{1}{(x-2)^2} = +\infty \]
Limites no Infinito com Funções Racionais
Exemplo 3:
\[ \lim_{x \to \infty} \frac{3x^2 + 1}{x^2 - 5} \]
Neste tipo de limite, usamos os termos de maior grau (pois dominam o crescimento):
Numerador: \( 3x^2 \)
Denominador: \( x^2 \)
\[ \frac{3x^2 + 1}{x^2 - 5} \approx \frac{3x^2}{x^2} = 3 \]
\[ \lim_{x \to \infty} \frac{3x^2 + 1}{x^2 - 5} = 3 \]